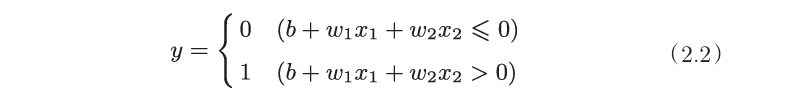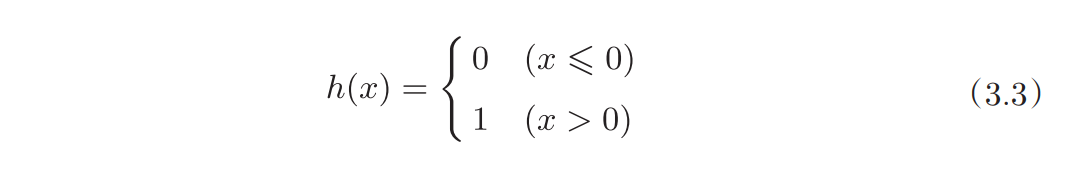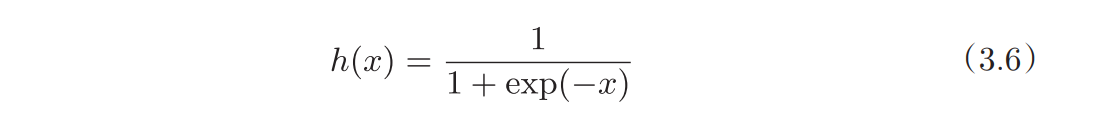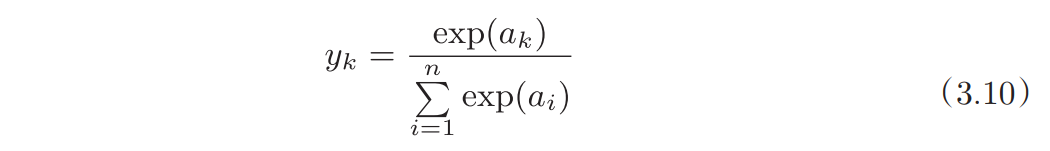简易神经网络_学习(SGD方法)
正者,正也。其心以为不然者,天门弗开矣。
作为《深度学习入门》的阅读笔记,本文简略概述深度学习的学习过程,损失函数,梯度法相关的内容,并辅以python实现
需要事先了解的
本文并不是从零开始的,需要实现了解
蜻蜓点水python
- 蜻蜓点水python_dlc
- 简略感知机
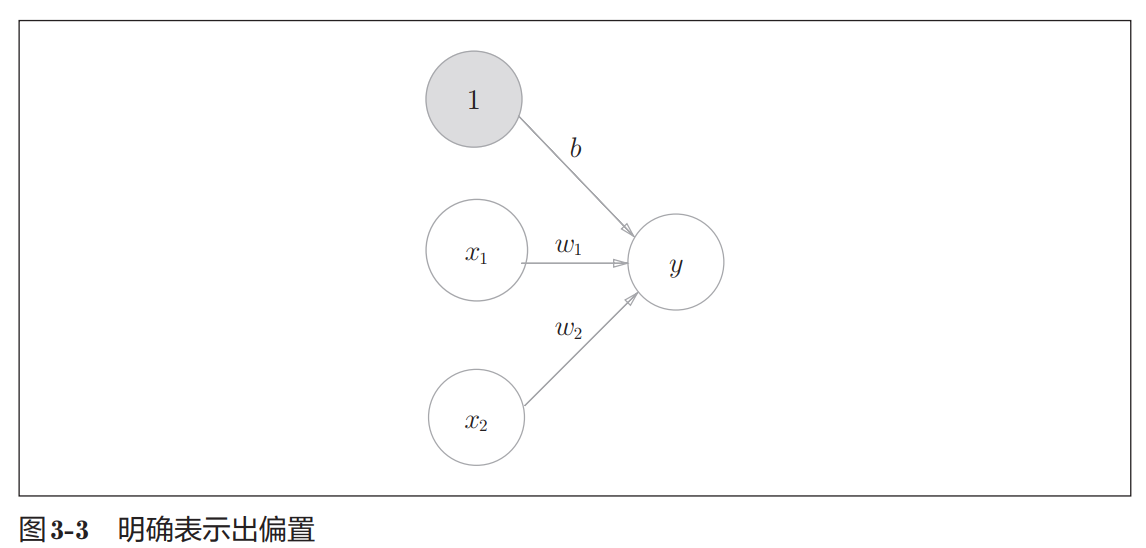
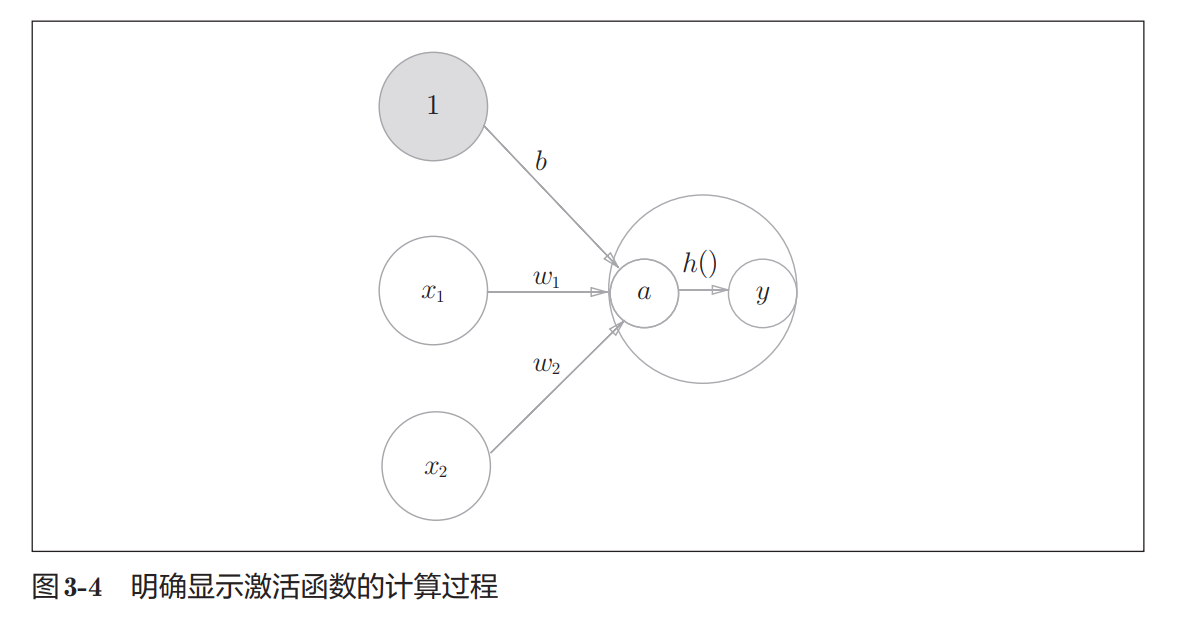
- 简易神经网络_推理和正向传播
不同的学习
首先,学习有不同的类型,人想,机器学习,深度学习;
然后,学习的基础是特征向量,机器学习中特征量还是人想出来的,深度学习则没有这一步骤,基本实现了全程机器管理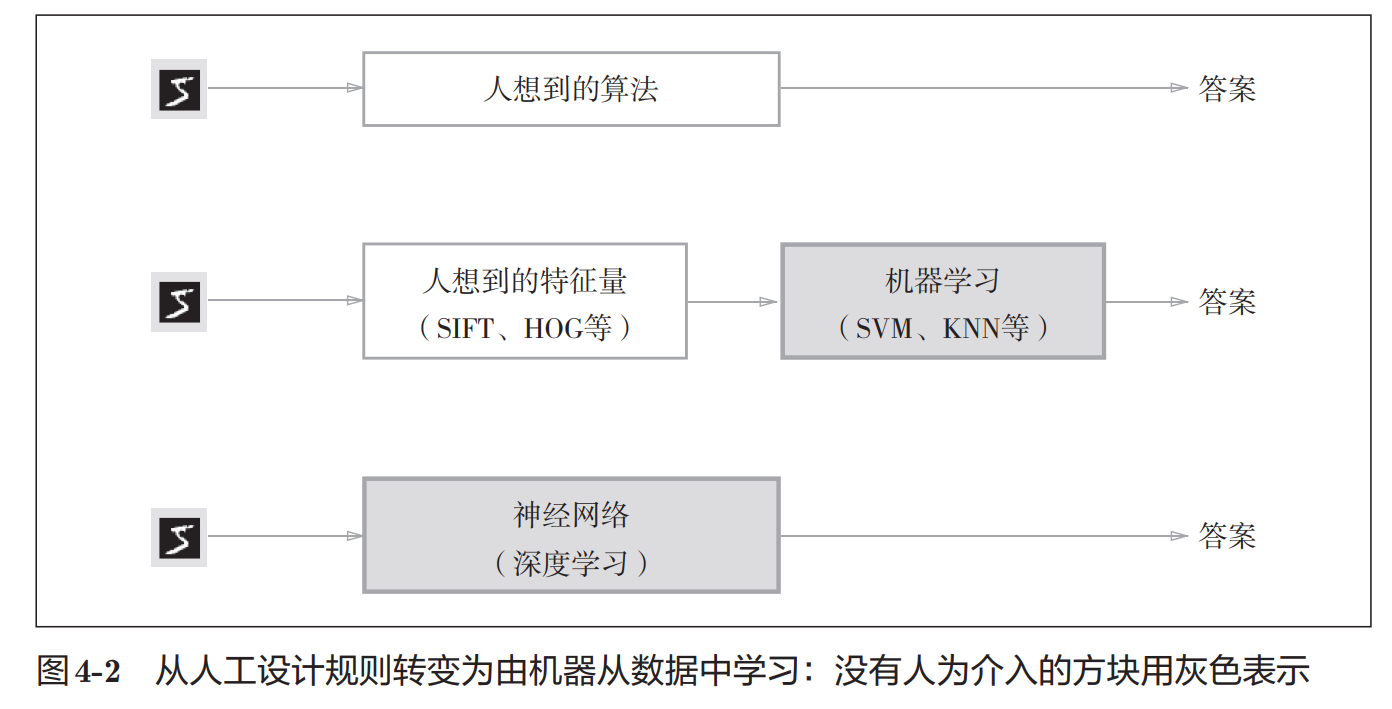
损失函数
有道是能观测就能干涉,能干涉就能控制;那么应该观测什么变量才能知道学习的进度,从而干涉和控制学习的过程呢?这里直接给出答案:损失函数。损失函数理论上可以使用任何函数,这里使用均方误差和交叉熵误差 。
这里有一个问题,为什么不使用精度(即准确度)来最为指标呢?首先说结论:在进行神经网络的学习时,不能将识别精度作为指标,并且对于大部分导数(后面会提到)为0的函数,都不能作为指标,会导致学习无法进行(无法更新参数),原因在了解学习的过程后自然能理解。
均方误差
直接公式,实现如下: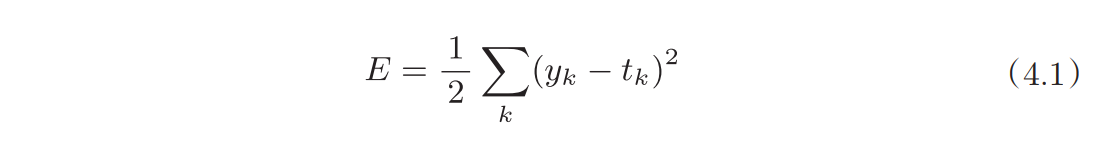
- y_k是前向传播的输出
- t_k是监督数据的标签(一般是one-hot表示)
- k是维度
import numpy as np
def mean_squared_error(y, t):
return 0.5 * np.sum((y-t)**2)
print(mean_squared_error(np.array([0.1,0.7,0.2]),np.array([0,1,0]))) #判断正确
print(mean_squared_error(np.array([0.1,0.7,0.2]),np.array([1,0,0]))) #判断错误
#0.07000000000000002
#0.67可以看出,如果判断正确,损失函数会是一个较小的数字,如果判断失败,损失函数会是一个较大的数字。
交叉熵误差
直接公式,实现如下: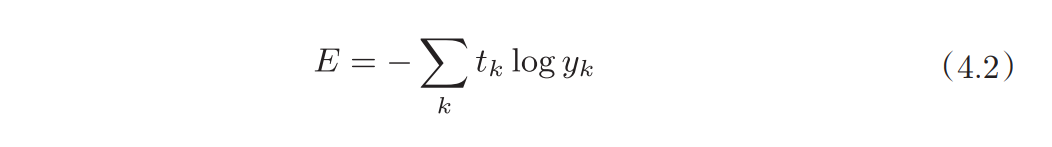
- y_k是前向传播的输出
- t_k是监督数据的标签(一般是one-hot表示)
- k是维度
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta))
print(cross_entropy_error(np.array([0.1,0.7,0.2]),np.array([0,1,0])))
print(cross_entropy_error(np.array([0.1,0.7,0.2]),np.array([1,0,0])))
#0.3566748010815999
#2.302584092994546- 其中delta是为了避免log的参数有0的情况
Mini-Batch学习
和推理的过程一样,学习也可以用批处理的方法完成,不过实现上有些区别;这里以交叉熵误差为例
第一个是损失函数公式的变化: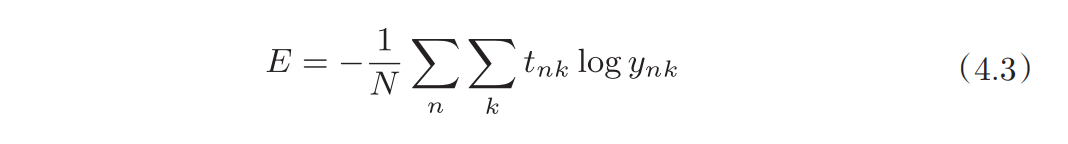
可见其实就是取平均,实现如下:
def cross_entropy_error2(y, t):
batch_size = 1
if y.ndim > 1:
batch_size = y.shape[0]
return -np.sum(t * np.log(y + 1e-7)) / batch_size
#测试不同维度
print(cross_entropy_error2(np.array([0.1,0.7,0.2]),np.array([0,1,0])))
print(cross_entropy_error2(np.array([0.1,0.7,0.2]),np.array([1,0,0])))
print(cross_entropy_error2(np.array([[0.1,0.7,0.2],[0.1,0.7,0.2]]),np.array([[0,1,0],[0,1,0]])))
print(cross_entropy_error2(np.array([[0.1,0.7,0.2],[0.1,0.7,0.2]]),np.array([[1,0,0],[1,0,0]])))第二个是训练数据其实还是很多的,想一次性全部学习是高耗能甚至有些不现实的,所以需要使用np.random.choice抽取一个batch来学习
# 这里的路径按本地实际来
from dfs.dataset.mnist import load_mnist
import sys,os
sys.path.append(os.pardir)
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True,
normalize=False,one_hot_label=True)
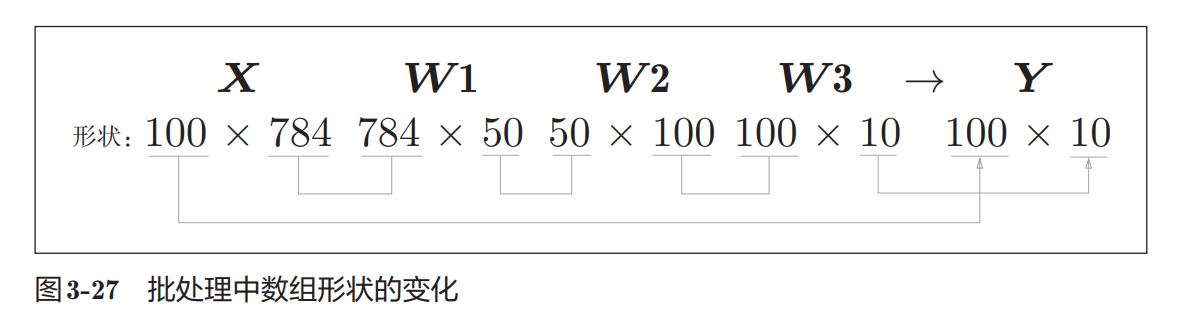
# 输出各个数据的形状
print(x_train.shape) # (60000, 784)
# 输出各个数据的形状
print(t_train.shape) # (60000,)
print(x_test.shape) # (10000, 784)
print(t_test.shape) # (10000,)
train_size = x_train.shape[0]
batch_size = 10
batch_mask = np.random.choice(train_size, batch_size)
print(batch_mask) # 输出抽选的索引
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
print(x_batch.shape) # (10, 784)
print(t_batch.shape) # (10,)
#(60000, 784)
#(60000, 10)
#(10000, 784)
#(10000, 10)
#[ 6681 4809 12952 4669 1444 20997 56685 39195 24206 8649]
#(10, 784)
#(10, 10)第三如果标签不是one-hot表示,有那么一个特殊的实现方法,思路是虽然是求和,但只有正确项会有值
def cross_entropy_error2(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
print(y[np.arange(batch_size), t])
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
print(cross_entropy_error2(np.array([[0.1,0.7,0.2],[0.1,0.7,0.2]]),np.array([1,2])))
#[0.7 0.2]
#0.9830561067579126另外有个概念会在后面用到这里先提出:
epoch是一个单位。一个epoch表示学习中所有训练数据均被使用过一次时的更新次数。比如,对于 10000笔训练数据,用大小为 100笔数据的mini-batch进行学习时,重复随机梯度下降法100次,所有的训练数据就都被“看过”了 。此时,100次就是一个epoch。
导数和梯度
有了损失函数,就可以观测学习的进度,但是如何在此基础上对其进行控制呢?要做到这点需要解决三个问题,函数的值是会通过自变量的变化而变化的,改哪个变量会使损失函数变小?如何改?要改多少?
直接说结论:修改的变量是权重和偏置,依靠导数计算出的梯度来修改自变量,改多少依赖于人工设定的学习率。
导数
不准确的说,导数就是x周围很小范围的斜率(中心差分),既不是x左边的斜率也不是x右边的斜率(前向差分);数值微分和真实的解析解必然是有所差距的。
求导数的实现如下:
def numerical_diff(f,x,h=1e-4):
return (f(x+h)-f(x-h))/(2*h)
def func_test(x):
return 2*x+1
numerical_diff(func_test,np.array([2,3]))偏导数和梯度
多个变量的函数的导数就是偏导数,当然一个偏导数只能对其中一个变量来做,另外的变量就当作常数对待,称为函数对该变量的偏导数,这是解析解的做法;对于数值解则更加的简单一点,固定其他变量,只变化一个变量来求导数就是函数针对这个变量的偏导数。
把所有变量的偏导数组成向量,就是梯度,梯度指向的方向是函数变化(增加)率最大的方向。所以对其取负数,就是损失函数下降最快的方向。
实现如下:
def numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x)
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
idx = it.multi_index
tmp_val = x[idx]
x[idx] = float(tmp_val) + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 还原值
it.iternext()
return grad
def test_func(x):
return x[0]*x[0]+x[1]*x[1]
numerical_gradient(test_func,np.array([3.0,4.0]))
#array([6., 8.])- NumPy 迭代器对象
numpy.nditer提供了一种灵活访问一个或者多个数组元素的方式。见NumPy 迭代数组 | 菜鸟教程
梯度下降法
按上述说的,按照梯度反方向更新参数就是梯度下降法,公式如下:
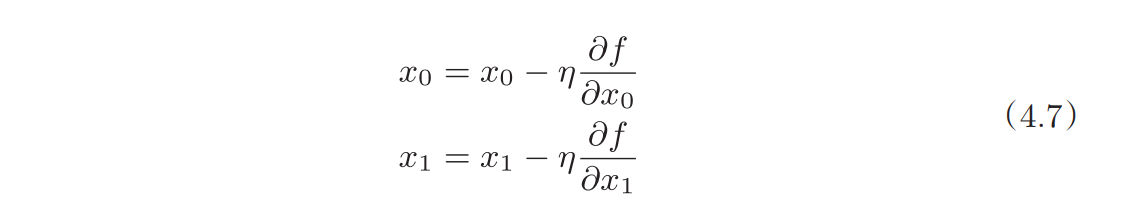
其中偏导数前面的常数就是学习率,人为指定,规定学习的程度,过大过小都不好,这里默认0.01,实现如下:
def gradient_descent(f,init_x,lr=0.01,step_num=100):
x = init_x
for i in range(step_num):
grad = numerical_gradient(f,x)
x -= lr*grad
return x
def function_2(x):
return x[0]*x[0]+x[1]*x[1]
init_x=np.array([-3.0,4.0])
gradient_descent(function_2,init_x,lr=0.1,step_num=100)
#array([-6.11110793e-10, 8.14814391e-10])另外,像这种人为指定的参数,称为超参数,像是mini-batch的大小,输入的形状,学习的次数都是超参数
总结和实现
现在就可以继续上章,完成MINIST的学习步骤了,但是还有一些细节需要说明
神经网络的梯度法
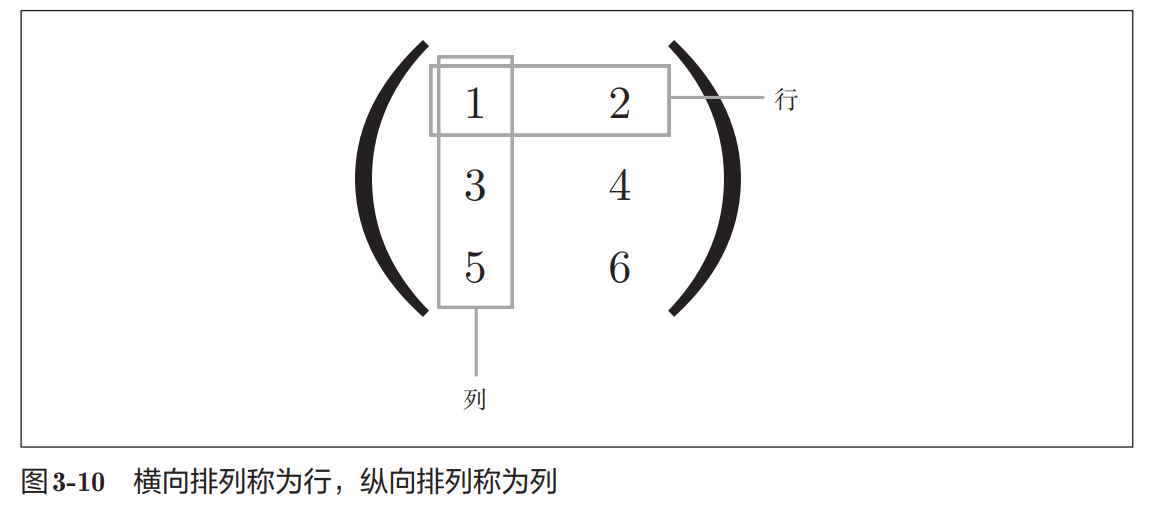
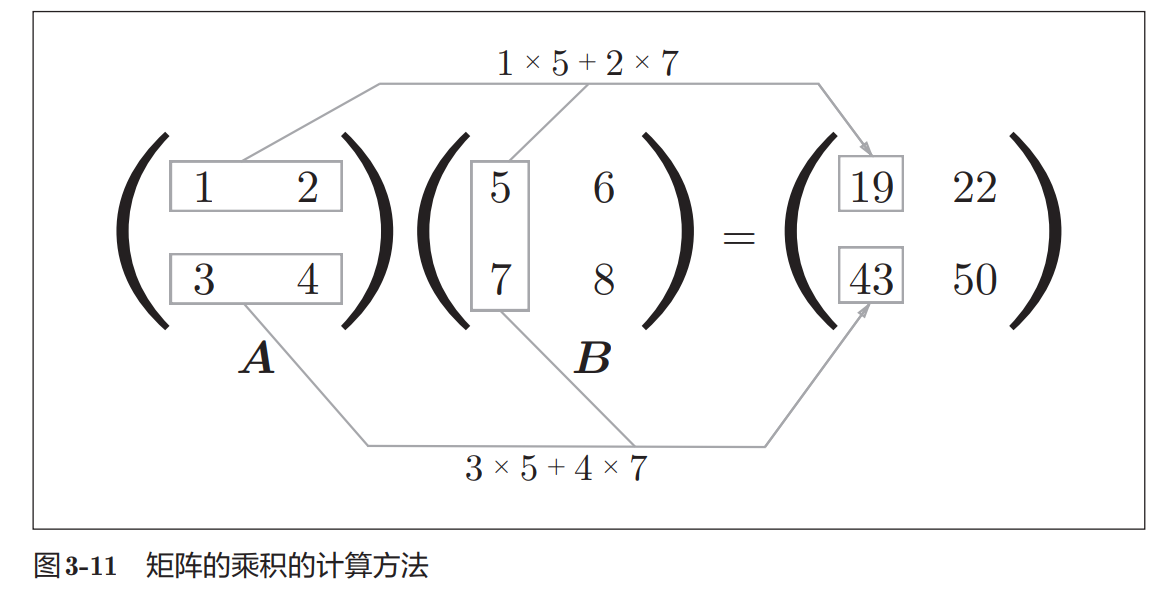
在实际的神经网络中要求的是损失函数对于权重的梯度,也就是对权重矩阵中的每个成员求梯度,最后结果还是矩阵:

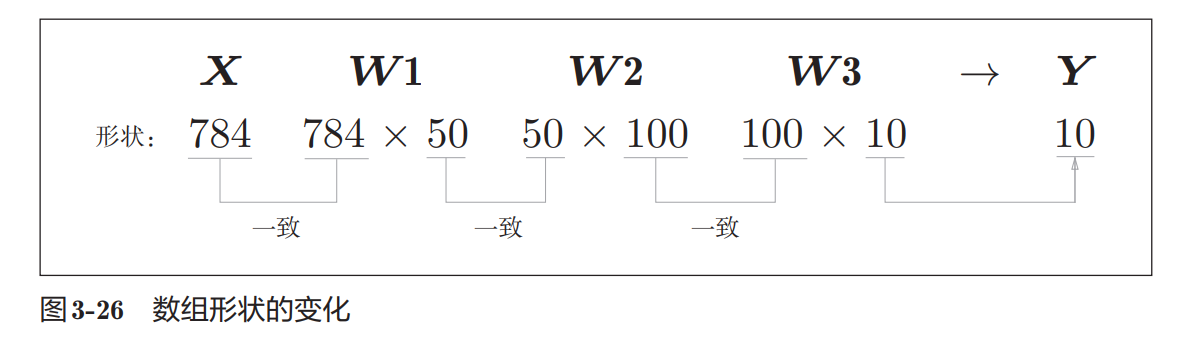
对于实现而言,只要能保证矩阵的形状没有问题即可
学习算法的步骤

步骤4则是重复1-3的步骤
而这种随机选取+计算梯度的方法称为:随机梯度下降法(SGD)
实现
先列出代码
# 这里的路径按本地实际来
import numpy as np
from dfs.dataset.mnist import load_mnist
import sys,os
sys.path.append(os.pardir)
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True,
normalize=False,one_hot_label=True)
# 输出各个数据的形状
#print(x_train.shape) # (60000, 784)
# 输出各个数据的形状
#print(t_train.shape) # (60000,10)
#print(x_test.shape) # (10000, 784)
#print(t_test.shape) # (10000,10)
train_size = x_train.shape[0]
batch_size = 10
batch_mask = np.random.choice(train_size, batch_size)
#print(batch_mask)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
print(x_batch.shape) # (10, 784)
print(t_batch.shape) # (10,10)
def cross_entropy_error(y, t):
batch_size = 1
if y.ndim > 1:
batch_size = y.shape[0]
return -np.sum(t * np.log(y + 1e-7)) / batch_size
def softmax(a):
c = np.max(a)
exp_a = np.exp(a-c) #溢出对策
sum_exp_a = np.sum(exp_a)
y = exp_a /sum_exp_a
return y
def sigmoid(x):
return 1/(1+np.exp(-x))
class SigMoidLayer:
def __init__(self,w,b,s="SigMoid"):
self.layer_name = s
self.w=w
self.b = b
def forward(self,x):
a=np.dot(x,self.w)+self.b
return sigmoid(a)
class OutputLayer2:
def __init__(self,w,b,s="Ouput"):
self.layer_name = s
self.w=w
self.b = b
def forward(self,x):
a=np.dot(x,self.w)+self.b
return softmax(a)
def numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x)
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
idx = it.multi_index
tmp_val = x[idx]
x[idx] = float(tmp_val) + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 还原值
it.iternext()
return grad
class TestMNIST:
# 正常情况下,权重或者偏置都应该是学习的结果,这里直接赋值只是一种假设
def __init__(self):
self.rate=0.01
self.grads_b = {}
self.grads_w = {}
self.network_w = {}
self.network_b = {}
self.network_w['L1'] = np.random.randn(784,50)
self.network_b['L1'] = np.zeros(50)
self.network_w['L2'] = np.random.randn(50,100)
self.network_b['L2'] = np.zeros(100)
# 输出层
self.network_w['L3'] = np.random.randn(100,10)
self.network_b['L3'] = np.zeros(10)
self.layers=['L1','L2']
def forward(self,x):
tmp=x
for l in self.layers:
tmp = SigMoidLayer(self.network_w[l],self.network_b[l],l).forward(tmp)
#print(l,tmp)
tmp = OutputLayer2(self.network_w['L3'],self.network_b['L3'],'L3').forward(tmp)
return tmp
def loss(self,x,t):
return cross_entropy_error(self.forward(x),t)
def grad(self,x,t):
loss_W = lambda W: self.loss(x, t)
self.grads_w={}
self.grads_b={}
self.grads_w['L1']=numerical_gradient(loss_W,self.network_w['L1'])
self.grads_b['L1']=numerical_gradient(loss_W,self.network_b['L1'])
print('L1 Done.')
self.grads_w['L2']=numerical_gradient(loss_W,self.network_w['L2'])
self.grads_b['L2']=numerical_gradient(loss_W,self.network_b['L2'])
print('L2 Done.')
self.grads_w['L3']=numerical_gradient(loss_W,self.network_w['L3'])
self.grads_b['L3']=numerical_gradient(loss_W,self.network_b['L3'])
print('L3 Done.')
def update(self):
self.network_w['L1']-=self.rate*self.grads_w['L1']
self.network_b['L1']-=self.rate*self.grads_b['L1']
self.network_w['L2']-=self.rate*self.grads_w['L2']
self.network_b['L2']-=self.rate*self.grads_b['L2']
self.network_w['L3']-=self.rate*self.grads_w['L3']
self.network_b['L3']-=self.rate*self.grads_b['L3']
nett = TestMNIST()
#测试代码
#nett.forward(np.random.randn(100,784))
# 学习过程
mini_batch_size = x_train.shape[0]
select_size = 100
loss_point =[]
train_time=10000
for i in range(train_time):
# 选择数据
mask = np.random.choice(mini_batch_size, select_size)
x_batch = x_train[mask]
t_batch = t_train[mask]
print(x_batch.shape,t_batch.shape)
print("Loop",i+1)
# 损失函数
loss_p=nett.loss(x_batch,t_batch)
loss_point.append(loss_p)
print("Loss:",loss_p)
# 计算梯度
nett.grad(x_batch,t_batch)
# 更新参数
nett.update()
#推理过程
batch_size=100
accuracy_cnt=0
for i in range(0,len(x_test),batch_size):
x_batch = x_test[i:i+batch_size]
t_batch = t_test[i:i+batch_size]
y_batch = nett.forward(x_batch)
#print(y_batch.shape)
p=np.argmax(y_batch,axis=1)
t=np.argmax(t_batch,axis=1)
accuracy_cnt+=(np.sum(p==t)/batch_size)
print("Accuracy:" + str(float(accuracy_cnt) / (len(x_test)/batch_size)))
import matplotlib.pyplot as plt
# 生成数据
xx = np.arange(0, train_time)
# 绘制图形
plt.plot(xx, loss_point)
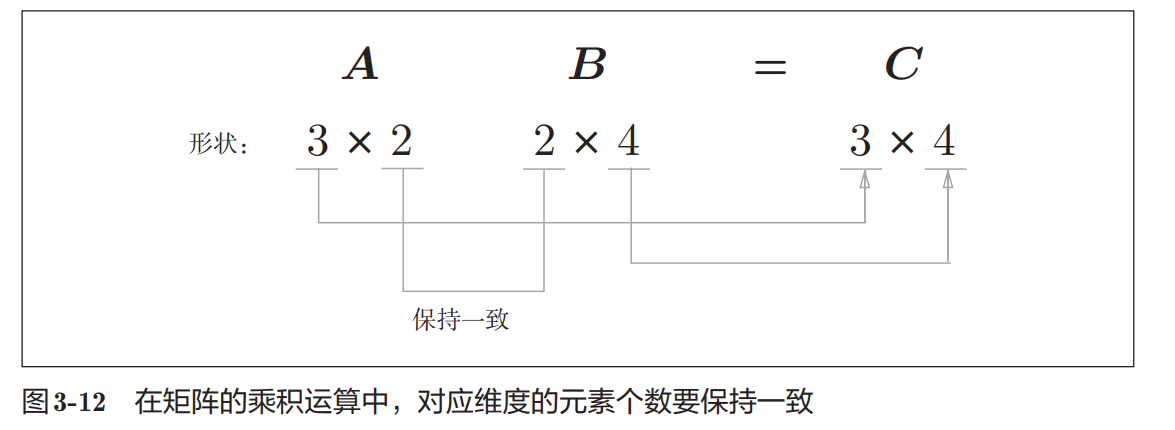
plt.show()首先要注意的是矩阵的形状一定要“严丝合缝”,这是做矩阵计算的基础
np.zeros(50)是创建0矩阵的方法,第一个参数是shape
- 然后当运行该代码时可以发现一点,就是随机梯度下降的处理速度十分缓慢,所以在之后会需要反向传播这一方法来加速梯度的计算
评价方法
评价一个神经网络的方法就是评价它的泛化能力,也就是对于陌生数据的识别精度:
- 如果只对训练数据识别精度较好,则是发生了过拟合
- 一般来说,当学习经过一个epoch,就可以对测试数据和训练数据进行推理,然后进行可视化对比,这里只给出伪代码:

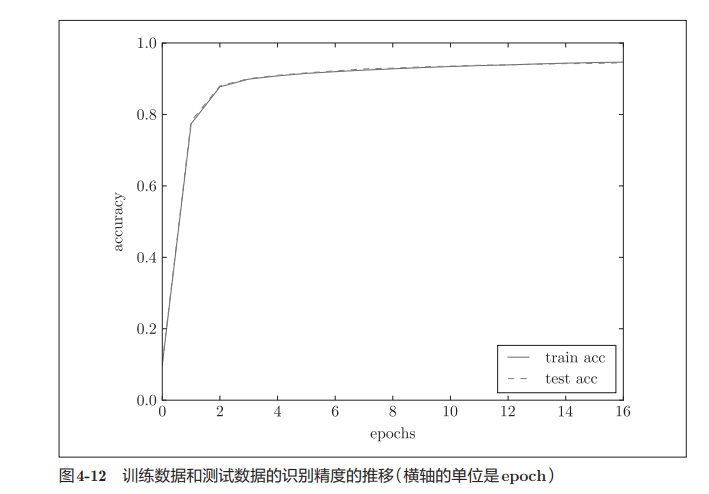
epoch是一个单位。一个epoch表示学习中所有训练数据均被使用过一次时的更新次数。比如,对于 10000笔训练数据,用大小为 100笔数据的mini-batch进行学习时,重复随机梯度下降法100次,所有的训练数据就都被“看过”了。此时,100次就是一个epoch。
不幸的结果
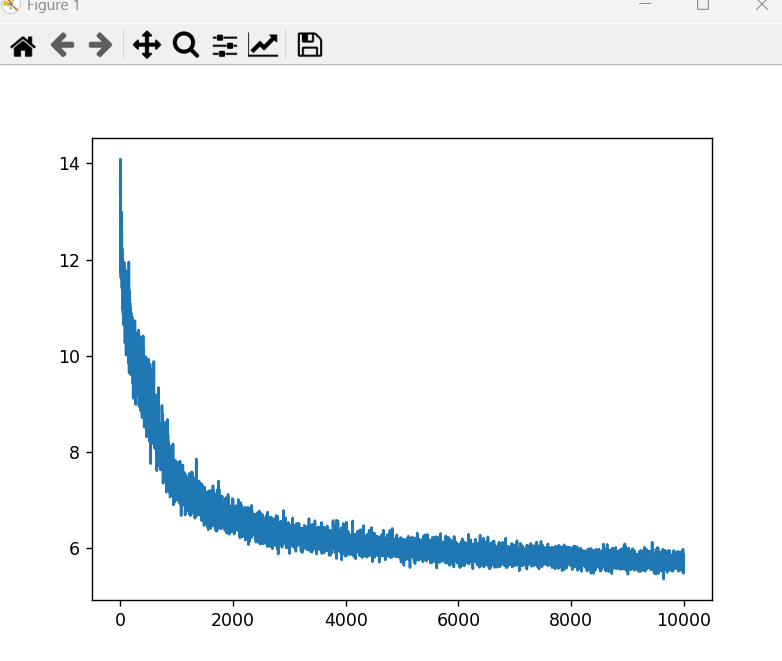
和原著对比,这里的效果差了很多(最重要的是运行时间巨长!!!!整整2个星期),原因会放在未来探索,可能的原因一方面是初始化参数的问题,一方面可能是层级结构的问题。准确度在:Accuracy:0.7011999999999997 而不是0.9以上,梯度下降的也不太对,如下图。
但不管怎么样,SGD是有效果的,接下来需要解决其速度太慢的问题。